Ｃフックに発生する応力の解析方法　　　　　　HOME　技術資料室 　技術用語 ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 　Ｃフックは簡単な構造ですが、重量物を頭上に持上げて運搬するものなので、破壊した場合には重大災害を招く危険があります。設計段階から金属疲労を考慮した強度設計が必要です（「Ｃフックの疲労破壊」参照） 　発生する応力の解析には、下記の二通りの方法がありますが、従来広く行われている材料力学モデルではでコーナー部の応力集中の影響などが加味されず、近似計算になります。最近精度の良さから機械の設計に広く使われている有限要素法 (FEM) が、Ｃフックにおいても広く適用されることが望まれます。 材料力学モデルによる解析 有限要素法 （FEM） による解析 　材料力学を使った解析方法ではＣフックを下図右のような梁構造（この場合はH ビーム）にモデル化して理論式によって発生する最大応力を計算します。 最大応力σ=(曲げモーメントM／断面係数Z )＋重力による応力 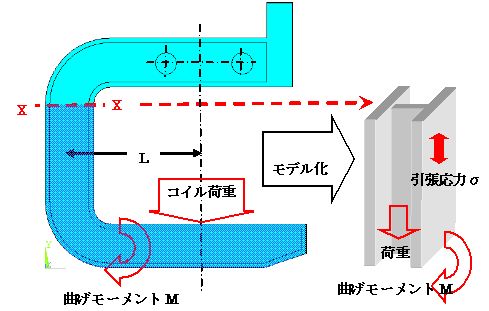　有限要素法とは構造物を下図左のような微小要素に分解し、それぞれの要素間の関係を数式化してコンピューターで解析する方式で、下図右のように全体の応力分布や最大応力値と発生箇所が精度良くわかるため、最適な構造設計が可能になります。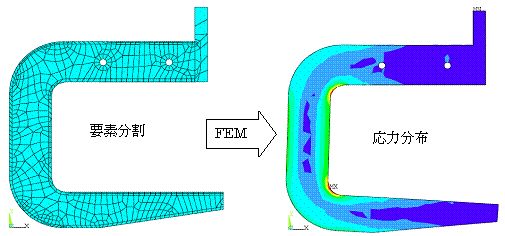（応力の分布を色で表示）　 　有限要素法は1950 年代にボーイング社が飛行機の設計用に開発したものですが、現在では CAD と共に機械や建築の設計にも広く使われています。 （計算例） 　 H ビーム断面寸法 300 mm B 90 mm h 240 mm b 24 mm W 最大コイル重量(20 ton) 196,000 N A 断面積 32,760 mm2 L1 縦ビーム長さ 1,130 mm L2 下部横ビーム長さ 1,600 mm L 荷重〜腕中心距離 900 mm w0 フック自重 w1 X-X断面下自重＝A×(L1+L2)×7.85／106 x 9.8 6,880 N w2 w1中曲げﾓｰﾒﾝﾄ寄与分＝A×L2×7.85／106x 9.8 4,032 N w3 X-X断面下荷重=W+w1 206,880 N M 重量による曲げﾓｰﾒﾝﾄ=L×w3 18,631,857 N-mm Z 断面係数＝(BH3+h3b)／6H 1,534,320 mm3 σ1 曲げﾓｰﾒﾝﾄによる応力＝M／Z 121.4 MPa σ2 垂直荷重による応力＝ w3／A 6.32 MPa σmax X-X断面での最大応力=σ1+σ2 127.7 MPa 　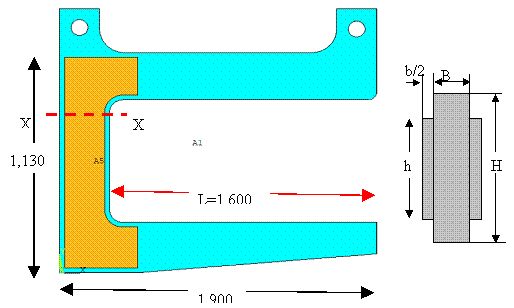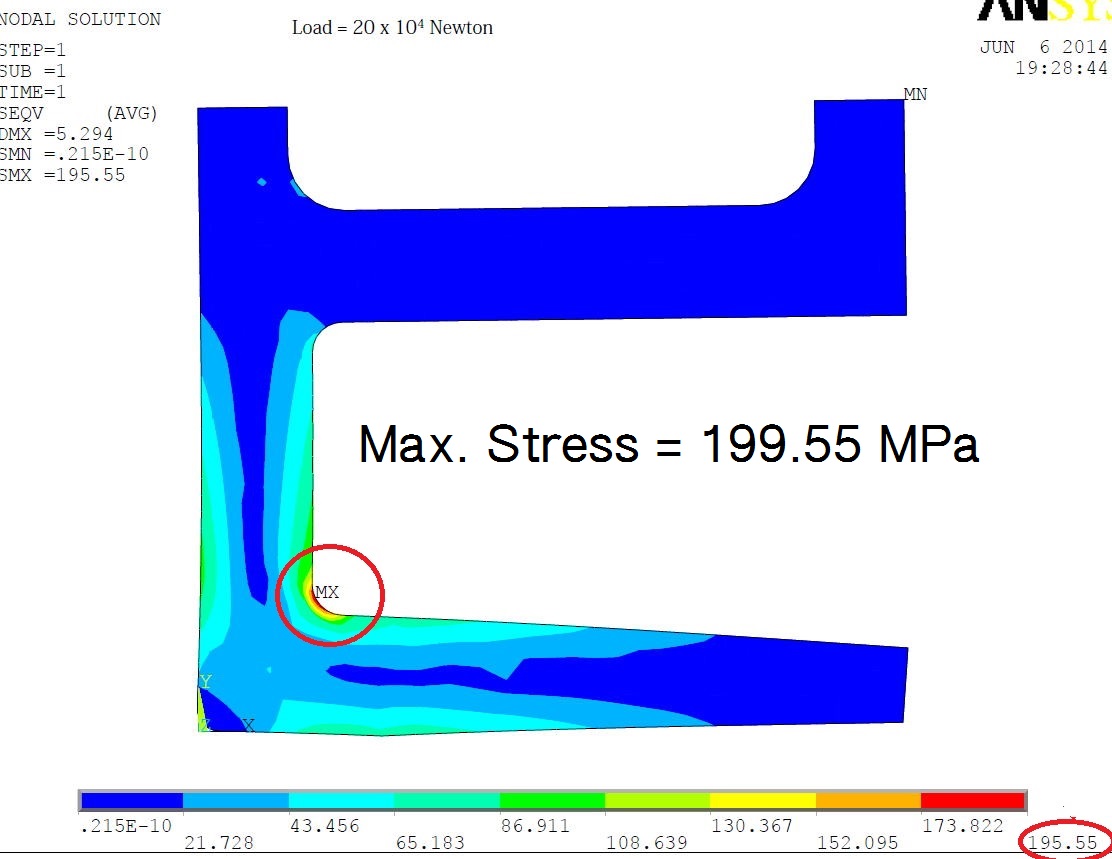このＣフックの場合、最大応力は上部コーナー内側で195.55 MPa が発生し、次に下コーナー部内側にもそれに近い応力が発生します。 　鋼材としてSS400 (初期抗張力TS≧400 MPa) を使用した場合の安全率は 400／195.55=2.04 しかなく、いずれ金属疲労が進んで鋼材の強度が40% (160 MPa) 近くまで落ちると折損の危険があります。 （考察） 　コーナー部の曲率半径は応力集中に大きな影響を与えますが、材料力学モデルでは曲率による応力集中が計算に入らないため、最大応力は FEM 方式に比較してかなり低く出ます。 HOME　技術資料室　Ｃフック診断