＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
ここで言うレベラーとは単体の形状矯正機としてのレベラーです。
１．レベラーの種類と特徴
一般的なレベラーとしては下記の３種類があります。
１) ローラーレベラー
２) テンションレベラー
３) ストレッチレベラー
１）ローラーレベラー
用途からの分類で、プロセッサー(ラフレベラー）とファインレベラーがあります。
下図は剪断ラインの例ですが、プロセッサーは主としてコイルの巻き癖を矯正する程度のもので、ロールの配列は通常2段(2-high)です。
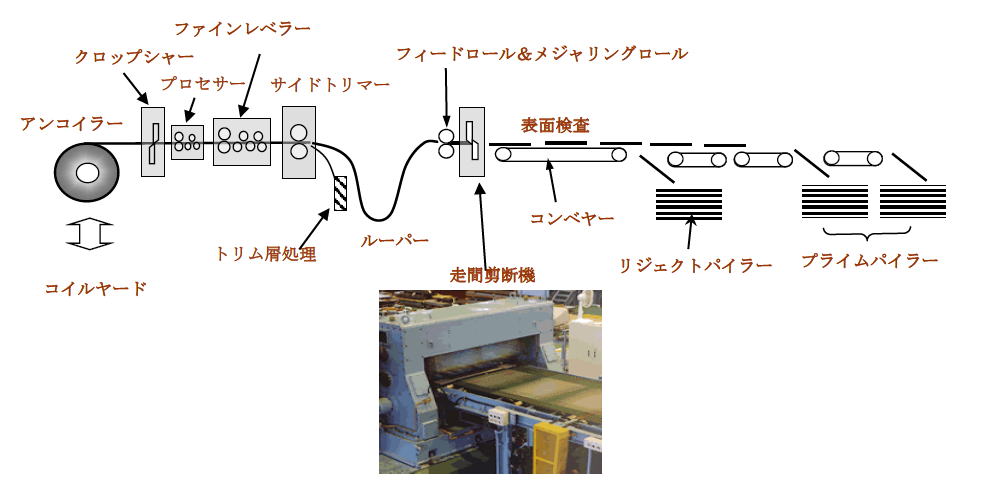
耳波・中伸びを矯正するためのローラーレベラーは通常ファインレベラーと呼ばれ、ロールの配列は下図のような4段（4-high) と6段 (6-high）の2種類があります。
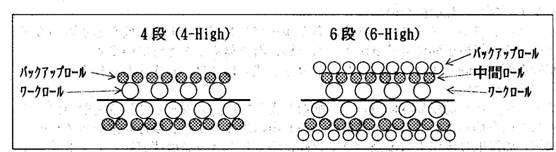
| (1) 4-high レベラー | ||
| 上下2段のワークロールとそれらを補強するためのバックアップロールが上下2段、計4段に配置されるため、4-highレベラーと呼ばれます。バックアップロールは一般的に4フィート幅の装置では幅方向に3列、6フィート幅の装置では5列配置されるのが一般的です。 バックアップロールの形状はある程度胴幅のある円筒 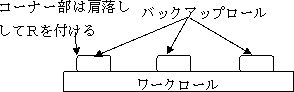 形や、あるいはベアリング等をそのまま使用したやや胴幅の狭いタイプがあります。バックアップロールの圧痕がワークロールに転写してタイガーマーク（下記２）になりやすいため、バックアップロールは右図のように、ある程度胴幅を持たせて、かつ両端コーナー部を肩落しして丸みを持たせておくことが必要です。 特に亜鉛めっき鋼板を通板する場合には、取れた亜鉛粉が研磨剤となってワークロールとバックアップロール間に磨耗痕を残す現象が出ます。 |
||
| (2) 6-high レベラー | ||
|
4-highレベラーのワークロールとバックアップロールの間に全幅の中間ロールを入れて、合計6段のロール群にしたものです。 バックアップロールの圧痕がワークロールに転写しにくい利点がありますが、長期的な使用に対してはバックアップロールは4-highの場合同様、幅広にしておくことが必要です。 |
||
| (3) | ワークロールの表面硬度：ショア硬度(Hs)で 90以上（バネ鋼に高周波焼入れ）更に硬質クロームメッキを掛ける場合が多い。 バックアップロールの表面硬度：ショア硬度(Hs)で60~70程度（S45Cが主体） |
|
| (4) その他の必要な機能 | ||
| ① |  塗油材⇒無塗油材に切り替える場合に、もっとも厄介なのがレベラー部です。ワークロールを初めバックアップロールにいたるまで油まみれになっているので、この油を取り除くことは困難な技術です。レベラー上部から洗浄剤を流して洗浄する方法やフェルトを噛ませて空転させながら左右に動かす装置（右写真）等がありますが、いずれも万全ではありません。 上下のロール郡をそれぞれカセットに組み込んで、塗油用と無塗油用の2セット常備しておくと、入れ替えるだけで短時間に切り替えができます。 |
|
| ② | 上部ロール群を短時間で開くような機構（クイックオープン）を入れておくと手入れ時等に有効です。 | |
２）テンションレベラー
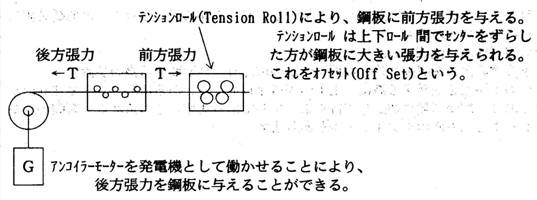
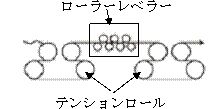鋼板に張力を掛けながらローラーレベラーを通板すると、形状の矯正が一層容易にできます。一般にはリコイリングラインにローラーレベラー及びその前後面にテンションロールを設置して、鋼板に張力を掛けながらローラーレベラーで繰返し曲げを掛けることで形状を矯正します。テンションを掛ける効果は、鋼板に発生する曲げ応力を高めて伸びやすくすることと、鋼板をレベラーロールの曲率に沿わせることにより曲げ応力がより強く掛けられるという効果です。
切板ラインでもアンコイラーとローラーレベラー後面のテンションロール（ピンチロールをやや強力にしたもの）の間でテンションを掛けながらレベラーを通板することで、形状矯正力を高めることが行われています。
３）ストレッチレベラー
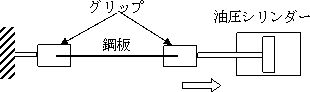デッドフラットが必要な切板では右図のような構造のストレッチレベラーで鋼板を引張って伸ばし、平坦な形状を得ていました。しかしながら、この方法では生産性が低い上に、鋼板の両端部にグリップマークが入るために、この部分を切り落とす必要があり、歩留も低い欠点がありました。テンションレベラーが実用化されて以後は、この方法は殆ど使われなくなりました。
２．ローラーレベラーによる形状矯正の原理
ローラーレベラーによる矯正機能には次の2種類があり、その原理は全く異なります。
1) 鋼板の「反り」の矯正
2) 鋼板の形状不良(「耳波｣､｢中伸び」）の矯正
１）「反り」の矯正(図-1） ローラーレベラー理論として解説されているものの多くが、この反りを直すことに関して説明しています。ローラーレベラーのワークロールによって、板が繰り返し曲げ変形を受けると、丁度針金を繰り返して曲げたときのように、だんだん柔らかくなってゆきます。この現象を『バウジンガー効果』といいますが、この原理を応用してレベラーの入側で強く圧下（インターメッシュ）を掛けて板を繰り返して曲げ、出側に近づくほど圧下を軽くしてゆくと図-1 に示すように板のそりは徐々にゼロに近づいて行きます。 |
||||||||||||||||||||
| ２）形状不良の矯正 | ||||||||||||||||||||
| (1) 形状不良とは(図-2） | ||||||||||||||||||||
 1枚の鋼板内の各部分で長さに違いがある場合には、板は平坦(フラット）にならず、板の端部が中央よりも長い場合は耳波、逆に中央部が端部よりも長い場合は中伸びになります。従って、1枚の板内の長さの差を取り除くことが形状をフラットにする原理です。 |
||||||||||||||||||||
| (2) なぜローラーレベラーで形状不良が直るか？(図-3、4） | ||||||||||||||||||||
 ローラーレベラーは図-3 のように、幅方向にバックアップロールが多数列配置されており、ワークロールの圧下量を板幅方向で変えることができます。今、上バックアップロールの中央部のみに圧下を掛けた場合を考えると、図-4 のように上のワークロールは中央部が下方向に押し下げられて湾曲した形となります。 レベラー中央部は上下のワークロールが食い込んだ配列となり、板の通る道程は端部よりも長くなるために、ここを通る板は端部より中央部に張力が掛かり、伸ばされます。 耳波の板の場合は、このように中央部を伸ばして端部と同じ長さにすることで耳波が矯正できます。 逆に、中伸びの板の場合はワークロールの端部に圧下を掛けることで、板の端部を伸ばして中央部と同じ長さにすることで、フラットな形状にすることができます。 この場合、板の長さを比較的容易に伸ばすことができりのは、上記の反りを直す場合と同様、ワークロールによる繰り返し曲げによる「バウジンガー効果」によって、板が柔らかくなり、変形しやすくなる効果があるからです。  ワークロールの径が小さいほど板の曲げ半径が小さくなるため、板の受ける歪が大きくなり、形状矯正能力は向上しますが、余りワークロール径が小さすぎると、ワークロールがバックアップロールの間で長さ方向に変形し、却って形状を崩す危険が出てきますので、おのずと限界があります。更に、板に張力を掛けながらレベラーを通すと、板がワークロールの径に密着して曲げられるために曲げ半径がより小さくなり、一層の形状矯正効果があります。このタイプのレベラーをテンションレベラーといい、平坦度やキャンバーの厳しい要求に対応する必要がある場合には必須の設備です。 尚、ローラーレベラーによるこれらの形状矯正は、いわば鋼板の内部を部分的に変形させて微妙にバランスさせることで保っている平坦度なので、この鋼板を再剪断して小切りするとこの内部応力（残留応力）が開放されて板がねじれたり、反ったりする危険があります。 テンションレベラーやスキンパス圧延での形状矯正では、板の全体を変形させて形状矯正するために、板内の残留応力は比較的小さく、この現象は余り生じません。 |
||||||||||||||||||||
３）ローラーレベラーの操作とインターメッシュの具体例 ＜インターメシュの定義＞ 上ワークロルの下面と下ワークロールの上面の間のギャップをインターメッシュと言い、通常間隔が空いている場合をプラス＋、締めこんだ方向をマイナスで表します。 上部のワークロールチョックや圧下装置にガタがあると、板を噛み込んだときに板の反力で上下ワークロール間のギャップが大きくなり、表示と異なってくるので注意が必要です。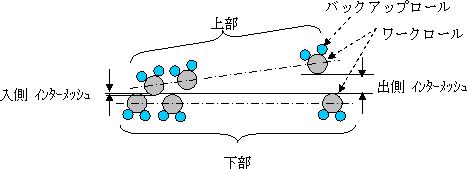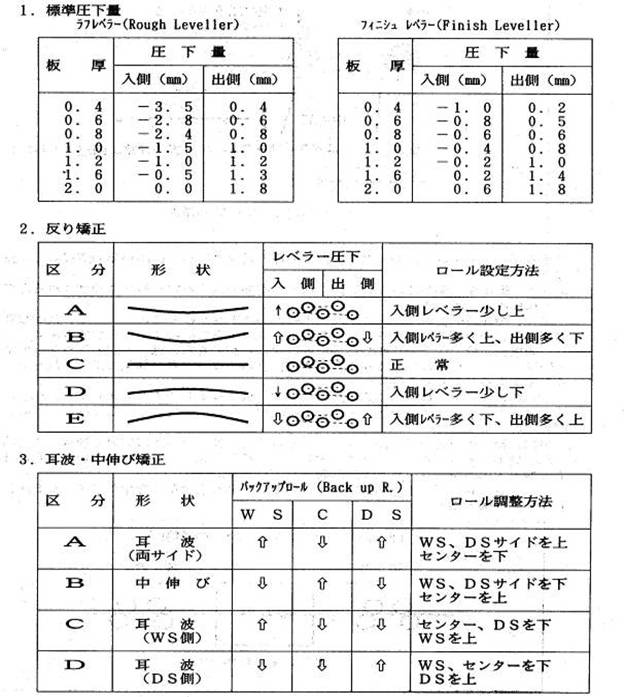  
|
||||||||||||||||||||
４）レベラーロールに掛かる力 ローラーレベラー装置においてインターメッシュ量によってワークロールが鋼板から受ける反力がどの程度になるかのシミュレーションを行いました。 ＜シミュレーションの方法＞ レベラーの構造は下図のように前提し、鋼板の幅及びワークロールの胴長は共に 1,000mm としました。各ワークロールに垂直荷重 p kgf を掛けたときに、上部ハウジングが何 mm下方に変位するかを有限要素法でシミュレーションしました。  
＜ワークロールに掛かる荷重と変位量の関係＞
但し、上表におけるワークロールの変位量は 3.2mm 厚の鋼板を挟んだ状態からの変位量を示すので、レベラーのインターメッシュとしては 3.2 ｍｍ からこの値を差し引いた値になります。 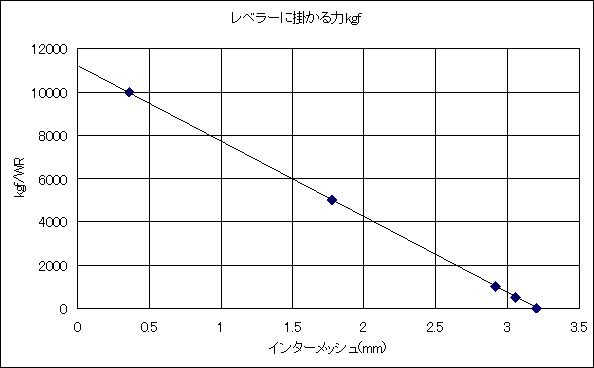 ＜ベアリングに掛かる荷重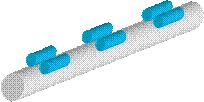＞  前提として各ワークロールが右図のように 2 個× 3 列のバックアップロールで補強されており、各バックアップロールは両端をローラーベアリングで固定されている構造の場合、
1 本のワークロールは自身のベアリング 2 個とバックアップロール 2個 × 3列 × 2個=12 個の合計 14 個のベアリングで支えられることになります。従って、平均的には1個のベアリングにかかる荷重はワークロールに掛かる荷重
p の 1 ／ 14 となります。例えば板厚 3.2mm ×板幅 1,000mm の鋼板に 0.5 mm のインターメッシュを掛けるとワークロールにかかる荷重はグラフから 10,000 ／ 2.841 × (3.2－0.5)＝ 9,500 kgfになるので、各ベアリングには平均的に 9,500 ／ 14 ＝ 679 kgf ＝ 6.6 kN の力が加わります。今、仮に荷重のピーク率を 2 とすると、上記の荷重は 6.6 kN × 2＝13.2 kN となり、これに見合う定格荷重のベアリングを使う必要があります。 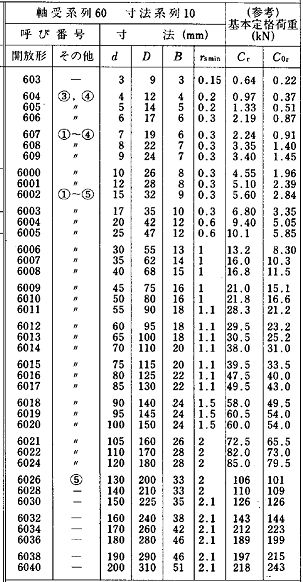 参考までにベアリングの基本定格荷重は参考値として各ベアリングメーカーがカタログに載せていますが、一例は右表のとおりです。但しベアリングの寿命は偏荷重を初め、色々な前提条件が複雑に絡み合うため、単純ではないようです。（ボールベアリング参照） |
||||||||||||||||||||
３．ローラーレベラーでの表面疵
| １）タイガーマーク (Tiger Mark) | |||
| (1) 発生原因 | |||
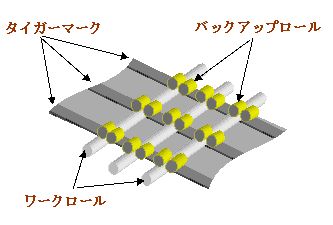 主として4-high レベラーの場合、バックアップロールがワークロールと接する部分はワークロールに磨耗痕が残り、製品に転写すると虎の模様のように長手方向に筋状の模様が入ります。程度がひどくなると、自動車などの大外板に使用した場合、塗装後にも跡が残る場合があります。特に亜鉛メッキ鋼板の通板が多くなると、亜鉛粉が一種の研磨剤の役目をするため、この現象が促進されるようです。 ロールベアリングをそのままバックアップロールとして使っている場合などは、幅が狭く硬質なため一層ワークロールに疵が入りやすい傾向があります。 |
|||
| (2) 対策 | |||
| ① | 6-highレベラーにするとバックアップの荷重は中間ロールで一旦受けてからワークロールにかかるため、磨耗痕は薄くなり製品に影響しにくくなります。但し、4-highからの改造は難しく新設する必要があります。 | ||
| ② | 4-highの場合でも、ワークロールをこまめに交換したり、レベラー圧下を極力軽くすることにより、ある程度の緊急避難は可能ですが、基本的にはワークロールの表面硬度をショアー硬度で90°以上にしてバックアップロールよりも硬くする必要があります。方法としては焼入れや窒化、ショットピーニング、硬質クロムメッキ等の方法がありますが、クロームメッキの場合でもある程度素地の硬度を上げてからメッキしないとメッキ層の寿命が短いようです。 | ||
| ③ | バックアップロールの幅を100mm以上程度に広くして、更に肩にRをつけるとある程度効果的ですが、既存設備からの改造は困難です。 | ||
| ２）停止マーク(Stop Mark) | |||
| (1) 発生原因 | |||
| レベラー部分に鋼板がはいったままで停止すると、レベラーワークロールの跡が幅方向に数本入る場合があります。特に塗装鋼板などの場合は対策が必要です。原因は一種の軽い圧痕又は折れで、外観上の問題です。 | |||
| (2) 対策 | |||
| ラインが停止しても、レベラー部では鋼板が停止しないよう、常に微速で動かすようにするのが一般的です。そのためには出側にループを設けて速度差を吸収する必要があります。 | |||
HOME 技術資料室 技術用語 剪断ライン